Circular coloring

In graph theory, circular coloring may be viewed as a refinement of usual graph coloring. The circular chromatic number of a graph $G$ , denoted 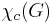$\chi_c(G)$ can be given by any of the following definitions, all of which are equivalent (for finite graphs).

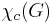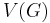1. $\chi_c(G)$ is the infimum over all real numbers $r$ so that there exists a map from $V(G)$ to a circle of circumference 1 with the property that any two adjacent vertices map to points at distance 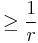$\ge \frac{1}{r}$ along this circle.

2. 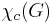$\chi_c(G)$ is the infimum over all rational numbers 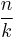$\frac{n}{k}$ so that there exists a map from 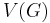$V(G)$ to the cyclic group 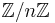${\mathbb Z}/n{\mathbb Z}$ with the property that adjacent vertices map to elements at distance 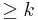$\ge k$ apart.

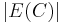3. In an oriented graph, declare the imbalance of a cycle $C$ to be $|E(C)|$ divided by the minimum of the number of edges directed clockwise and the number of edges directed counterclockwise. Define the imbalance of the oriented graph to be the maximum imbalance of a cycle. Now, 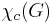$\chi_c(G)$ is the minimum imbalance of an orientation of $G$ .

It is relatively easy to see that 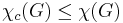$\chi_c(G) \le \chi(G)$ (especially using 1. or 2.), but in fact 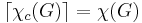$\lceil \chi_c(G) \rceil = \chi(G)$ . It is in this sense that we view circular chromatic number as a refinement of the usual chromatic number.

Coloring is dual to the subject of nowhere-zero flows and indeed, circular coloring has a natural dual notion: circular flows.

Circular coloring

See also